La domanda è ovviamente provocatoria, ma la risposta (negativa!?) non è poi così scontata, come cercheremo di dimostrare in questo articolo. Al di là delle battute, affronteremo un tema serio e di crescente e drammatica attualità: la discussione sui possibili scenari della sostenibilità del pianeta Terra nel XXI secolo.
Prendiamo spunto da un articolo sulla prima pagina del Corriere della Sera del 16 giugno 2008. L’autore, l’economista Giovanni Sartori, commenta con queste parole amare l’esito della riunione della FAO (Food and Agricolture Organization of the United Nations) di Roma (3-5.6.2008): «La grande carnevalata della FAO si è chiusa con la risibile e irresponsabile promessa di vincere la fame entro il 2050. Speriamo che prima venga chiusa la FAO». Citando il convegno indetto negli stessi giorni dalla Fondazione Aurelio Peccei per celebrare il 40° anniversario del Club di Roma, Sartori commenta: «i discorsi seri si fanno altrove» (16-17.6.2008), e prosegue: «Peccei fu il primo profeta della impossibilità di una crescita illimitata del pianeta Terra, così come due secoli fa il bravo abate Malthus fu il primo a intravedere la bomba demografica. Calcolò che mentre la popolazione poteva crescere in progressione geometrica (1,2,4,8), la produzione agricola può solo crescere in progressione aritmetica (1,2,3,4). Il suo Saggio sul principio di popolazione usciva nel 1798, prima della rivoluzione industriale. Ed è l’agricoltura meccanizzata, che Malthus non poteva prevedere, che ha rinviato di due secoli la resa dei conti. Ma ora ci siamo.
«La preoccupazione di Peccei e del Club di Roma fu diversa: segnalava l’imminente venir meno delle risorse naturali, e segnatamente del petrolio. Si capisce, consumiamo troppo perché siamo troppi. Ma nel 1972, quando uscì il primo rapporto, I limiti dello sviluppo, la popolazione mondiale era di 3 miliardi e 850 milioni. Vi rendete conto? In meno di quaranta anni si è quasi raddoppiata. […] ormai viviamo su una coperta troppo corta che se tirata da una parte lascia scoperta un’altra parte».
Già da questo stralcio si può intravedere come la matematica giochi un ruolo affatto marginale nel dibattito scottante circa la sostenibilità del nostro pianeta. E’ opportuno presentare brevemente gli attori citati da Sartori.
Thomas Malthus

Thomas R. Malthus (Londra 1766 – Haileybury 1834) fu professore di Economia Politica presso il college di Haileybury dove venivano formati i funzionari dell’East India Company. Nel 1798 pubblicò il volume Essay on the Principle of Population, che è citato dallo stesso Darwin nella sua autobiografia come un importante riferimento teorico per le sue ricerche.
In questo trattato Malthus introduce un primo modello matematico per lo studio dell’evoluzione di una popolazione. La questione si potrebbe sintetizzare in questi termini: c’è una “formula” che consenta di stimare il numero degli individui di una popolazione al variare del tempo?
I suoi studi lo portarono a prevedere l’arresto dello sviluppo economico a causa dell’incompatibilità fra la crescita demografica e la disponibilità di alimenti (crescita della popolazione in progressione geometrica, aumento della produzione agricola in progressione aritmetica).
Aurelio Peccei e il Club di Roma

Aurelio Peccei (Torino 1908 – Roma 1984), dirigente industriale (FIAT e Olivetti) in Italia e in America Latina; dal suo osservatorio privilegiato degli eventi internazionali comprese, già negli anni sessanta, che erano in corso mutamenti planetari che avrebbero dovuto essere affrontati con attenzione e coraggio. Nel 1968 fondò il Club di Roma, con lo scopo di riunire un gruppo di studiosi per un’analisi scientifica della situazione. La ricerca fu commissionata al System Dynamics Group della Sloan School of Management del MIT (Massachusetts Institute of Technology). I risultati, pubblicati nel trattato I limiti dello sviluppo (1972), produssero una tempesta, in particolare fra economisti. In un momento in cui l’economia spingeva verso un processo continuo di crescita appariva assurdo parlare di limiti e controllo.
Il libro fu un successo editoriale, con oltre trenta milioni di copie vendute in tutto il mondo, ma gli attacchi e l’ironia del mondo accademico amareggiarono Peccei finché visse. Oggi, a più di trent’anni di distanza, i numeri sembrano dargli ragione.
Il gruppo di Dennis Meadows

La ricerca commissionata dal Club di Roma fu svolta da un gruppo internazionale di giovani ricercatori diretto da Dennis Meadows, docente di System Management nell’università del New Hampshire.
Il problema affrontato si può riassumere nelle questioni seguenti: le politiche attuali portano ad un futuro sostenibile o al collasso? Cosa si può fare per creare un’economia umana che provveda ai bisogni di tutti?
Lo studio fu svolto ricorrendo ad opportuni modelli matematici elaborati mediante un potente calcolatore creato ad hoc, il World3.
Nel trattato I limiti dello sviluppo sono analizzati dodici scenari che illustrano differenti possibili modelli di sviluppo globale nell’arco di due secoli, dal 1900 al 2100. L’analisi è centrata soprattutto sui limiti fisici del pianeta, in particolare sulle risorse naturali esauribili, e sulla capacità non infinita della Terra di assorbire le emissioni industriali e agricole. Ogni scenario realistico mostra che questi limiti avrebbero costretto la crescita a fermarsi nel corso del XXI secolo. Nello scenario più pessimistico il libro colloca la fine della crescita intorno al 2015, un tempo che sembrava sufficiente per riflettere, scegliere e adottare misure correttive anche su scala globale. Due aggiornamenti sono seguiti al primo trattato ed entrambi confermano sostanzialmente le previsioni di questo.
Nello studio Oltre i limiti dello sviluppo (1992) sono analizzati gli sviluppi globali tra il 1970 e il 1990, evidenziando un’importante novità: l’umanità aveva ormai superato i limiti della capacità di sostentamento della Terra e si stava addentrando nel terreno della insostenibilità.
L’ultimo rapporto I nuovi limiti dello sviluppo (2006) prospetta una visione ancora più pessimistica di quelle precedenti.
Capacità di carico della terra – Impronta ecologica
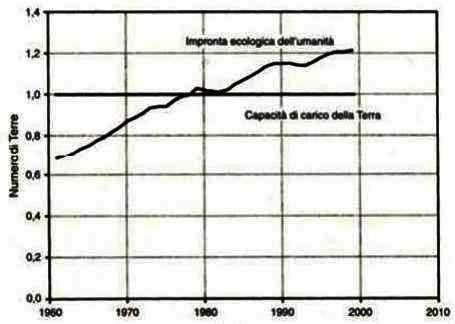
L’impronta ecologica è la porzione di superficie terrestre che occorrerebbe per produrre le risorse (cereali, foraggio, legname, pesce e superficie urbana) e per assorbire le emissioni (diossido di carbonio) della popolazione globale.
Il diagramma a lato mostra che la domanda umana ha superato le risorse naturali già a partire dagli anni Ottanta, mentre all’inizio del nuovo millennio raggiunge valori ad essa superiori del 20%.
Queste ricerche hanno consentito a Dennis Meadows di vincere lo scorso aprile il prestigioso Japan Prize Awards (500.000 $) della Science and Technology Foundation of Japan con la motivazione: «for transformation towards a sustainable society in harmony with nature». Purtroppo la consapevolezza collettiva del problema è gravemente limitata, come afferma lo stesso Meadows nell’intervista video che si può scaricare nel sito www.japanprize.jp
Il modello di evoluzione di Malthus
Il modello si propone di studiare la dinamica dell’evoluzione di una popolazione. Precisamente si propone di individuare una formula che consenta di stimare il numero degli individui al variare del tempo.
Assumiamo, ad esempio, che il tempo sia scandito in anni e denotiamo con 0P la consistenza iniziale (numero di individui allo stadio 0). Al termine del primo anno la popolazione sarà passata da P0 a P1, con un incremento ΔP=P 1−P0, detto tasso di crescita.
Dopo il secondo anno la popolazione avrà raggiunto la quota di P2 individui con tasso di crescita ΔP=P2 −P1 e così via. Il tasso di crescita sarà positivo nel caso di aumento della popolazione, negativo in caso di diminuzione, o nullo nel caso in cui il numero di individui si mantenga costante (situazione stazionaria).
L’evoluzione teorica della popolazione, descritta dalla sequenza P0, P1, P2,….., Pn, … dipende in modo determinante da quale tipo di tasso di crescita venga assunto.
Il caso più semplice è quello rappresentato da un tasso di crescita costante.
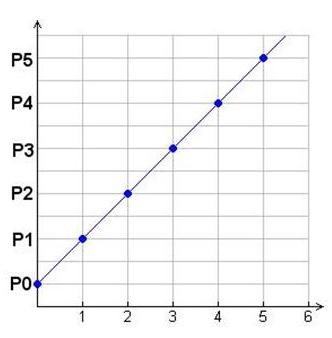
ΔP= Pn+1 – Pn = k
n=0,1,2….
Il numero degli individui, al variare del tempo, è quindi descritto dalla progressione aritmetica:
P0, P1 = P0 + k, P2 = P0 + 2k P3 = P0 + 3k
La formula che descrive sinteticamente il processo di evoluzione è quindi:
Pn = P0 + n*k n= 0,1,2,…
Dalla formula appare chiaro che la crescita (rispetto al valore iniziale) è proporzionale al tempo:
Pn – P0 = n*k n= 0,1,2,…
Così, ad esempio, si può stimare che in dieci anni la popolazione sarà cresciuta dieci volte quanto è aumentata in un anno.
Infatti, come evidenziato dal grafico, la sequenza (Pn)n si dispone lungo una retta, precisamente la retta di equazione:
y = P0 + k*x
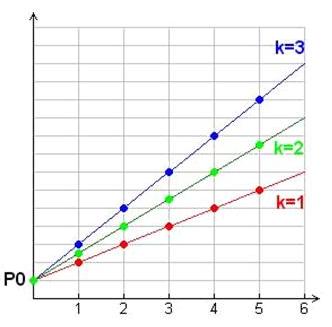
Il parametro k (coefficiente angolare della retta) descrive la velocità di crescita, come appare chiaro dal grafico a lato in cui sono messi a confronto modelli di evoluzione con diversi tassi di crescita . Il modello consente anche di valutare quanto tempo occorra affinché la popolazione raggiunga una data soglia S.
Per rispondere a tale quesito è sufficiente risolvere l’equazione:
P0 + n*k = S n = P0 / S*k
Il tempo necessario è allora inversamente proporzionale al fattore di crescita. In altri termini, un tasso di crescita più elevato consente di raggiungere la soglia in un tempo più breve.
Malthus formula la seguente ipotesi: il tasso di crescita è direttamente proporzionale al numero di individui.
L’ipotesi è ragionevole, in particolare se ricondotta ad una popolazione isolata, cioè una popolazione che non abbia scambi con l’esterno né in termini di risorse (limitazione del cibo o delle risorse naturali, inquinamento, vincoli economici, limiti indotti dalle forme di organizzazione sociale), né in termini di individui (immigrazioni, emigrazioni).
L’ipotesi di Malthus si traduce in termini matematici nella relazione:
ΔP = Pn+1 – Pn = a* Pn
o nella formula equivalente:
Pn+1 = Pn + a* Pn = (1+a) Pn
ove a è una costante di proporzionalità.
L’evoluzione di una popolazione isolata è quindi descritta dalla progressione geometrica P0, P1 = (1+a)P0, P2 = (1+a)2P0, P3 = (1+a)3P0, … ovvero dalla formula seguente Pn = (1+a)nP0 n = 0,1,2,…
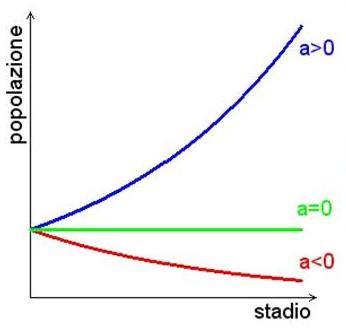
La costante a è detta fattore di crescita.
In questo caso, la sequenza (Pn)n ha come “curva sostegno” una curva esponenziale, precisamente il grafico della funzione:
f(x) = P0*(1+a)x
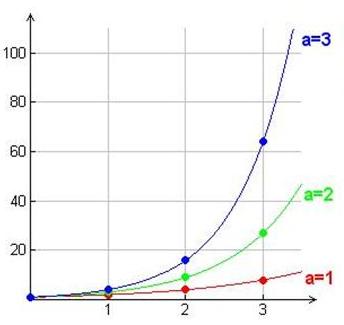
Dal parametro a dipende fortemente la velocità di crescita, come appare chiaro dal grafico a lato, in cui sono messe a confronto le diverse evoluzioni di popolazioni con pari consistenza iniziale, ma diversi fattori di crescita.
Tenuto conto delle proprietà della funzione esponenziale, le possibili evoluzioni sono sintetizzate in I nuovi limiti dello sviluppo e nel grafico seguenti.
Evoluzione di una popolazione:
Fattore di crescita-Evoluzione del processo
-1 < a < 0 estinzione
a = 0 stazionario (crescita zero)
a > 0 esplosione
Crescita lineare e crescita esponenziale
Il secondo capitolo dei Nuovi limiti dello sviluppo ha per titolo: La crescita esponenziale come forza motrice, a dimostrazione dell’importanza del concetto nella tematica in oggetto.
«La causa prima del superamento dei limiti sono la crescita, l’accelerazione, la rapidità del cambiamento. E’ più di un secolo che molte caratteristiche fisiche del sistema globale sono in rapida crescita. Per esempio, popolazione, produzione alimentare, produzione industriale, consumo di risorse e inquinamento stanno tutti aumentando, in molti casi sempre più velocemente. Il loro incremento segue un andamento che i matematici definiscono crescita esponenziale. […]Eventi meteorologici estremi, oscillazioni economiche, trasformazioni tecnologiche, epidemie, disordini civili sono tutti fenomeni che possono spezzare, con lievi alti e bassi, la regolarità delle curve; ma, nell’insieme, la crescita esponenziale domina il comportamento del sistema socioeconomico sin dai tempi della rivoluzione industriale [cioè esattamente da quando Malthus ha introdotto il suo modello].
«In un pianeta finito, la crescita fisica non può andare avanti per sempre […]. Questo tipo di crescita ha caratteristiche sorprendenti, che la rendono molto difficile da disciplinare. […]Le quantità che crescono in modo esponenziale sono ingannevoli perché la maggior parte di noi concepisce la crescita come un processo lineare».
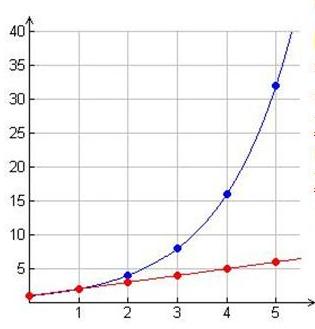
La profonda differenza fra crescita lineare e crescita esponenziale può essere illustrata dal grafico a lato in cui sono riportate le due sequenze citate espressamente da Peccei: in rosso la progressione aritmetica 1,2,3,4,… ovvero Xn = 1 + n n = 0, 1, 2, … in blu la progressione geometrica 1,2,4,8,… ovvero Xn = 2n n=0, 1, 2, …
A partire dal secondo stadio la crescita esponenziale ha la meglio sulla crescita lineare e il divario aumenta con il trascorrere del tempo.
Tempo di raddoppio
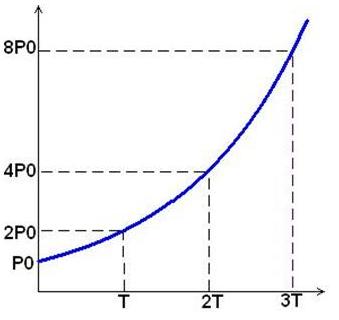
Sartori fornisce un dato significativo della crescita della popolazione mondiale, ricordando che in quarant’anni è quasi raddoppiata. Non si tratta di una semplice constatazione, in quanto il tempo di raddoppio (o quello di dimezzamento in caso di decrescita) è un parametro fondamentale per valutare la rapidità di evoluzione di un processo.
Precisamente il tempo di raddoppio T di una popolazione in espansione (a>0) è quello impiegato dal processo per raggiungere il doppio del valore iniziale.
Nel caso del modello di Malthus, grazie alla formula chiusa, il tempo di raddoppio è la soluzione di un’equazione esponenziale:
xo (1+a)T = 2×0 → T = log2/log(1+a) a > 0
Quest’ultima relazione evidenzia che il tempo di raddoppio è indipendente dal valore iniziale, ma dipende solo dal fattore di crescita “a”. Si tratta di un indice significativo del processo e viene adottato come una vera e propria unità di misura.
Tabuliamo alcuni valori della corrispondenza tasso di crescita – tempo di raddoppio:
In I nuovi limiti dello sviluppo è riportata la variazione del tasso di crescita e il relativo tempo di raddoppio della popolazione mondiale nel corso dei secoli:
a (%): 0,2 0,4 0,6 0,8 1 2
T (anni): 347174116 87 70 35
anno 1650-1900 1965-2000
Consistenza (miliardi) 0,5 1,6 3,3 6
Tasso di crescita (%) 0,3 0,7-0,82 1,2
Tempo di raddoppio (anni) 240 100 36 58
Il modello di Malthus è un esempio elementare di modello dinamico. Usando una metafora, possiamo dire che non si limita a descrivere una situazione scattando una fotografia, ma segue l’evoluzione del fenomeno in itinere, come se girasse un film. Il gruppo di ricercatori guidati da Meadows ha adottato proprio modelli dinamici (un po’ più complessi) per lo studio della sostenibilità del pianeta.
Alcuni fenomeni di crescita esponenziale tratti da I nuovi limiti dello sviluppo
Popolazione mondiale 1650-2050
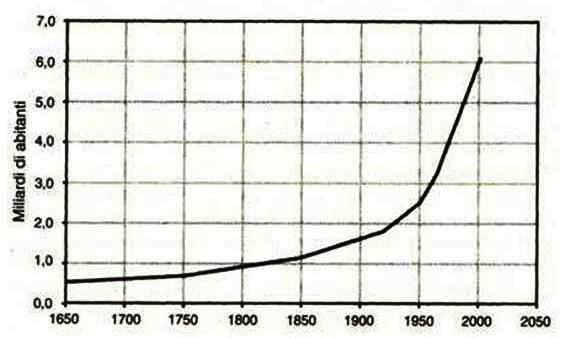
Dall’inizio della rivoluzione industriale, la popolazione della Terra è cresciuta in modo esponenziale, come mostra chiaramente la forma della curva e l’incremento della variazione nel tempo. Una stima del tempo di raddoppio della popolazione mondiale, effettuata nel 1994, lo valutava in soli 38 anni. Oggi però il tasso di crescita è in diminuzione. Nel 2001 era del 1,3% annuo, corrispondente a un tempo di raddoppio pari a 55 anni.
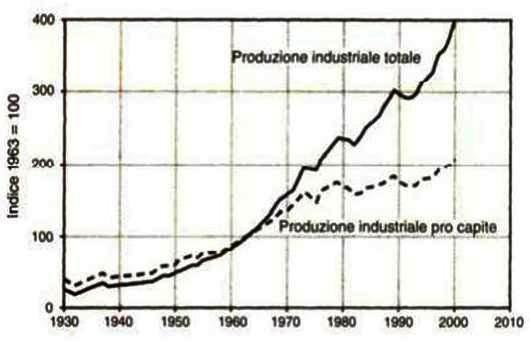
Produzione industriale 1930-2010
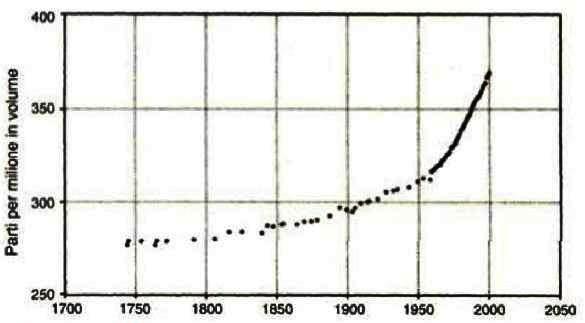
Concentrazione di diossido di carbonio nell’atmosfera 1700-2050
La concentrazione di diossido di carbonio (CO2):
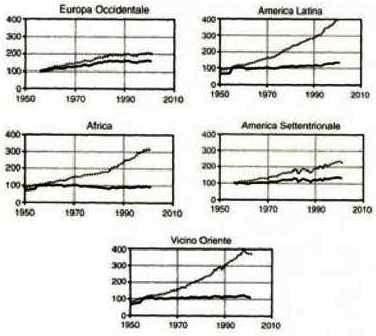
Indice di produzione alimentare 1950-2010
L’indice della produzione totale di alimenti è raddoppiato o triplicato negli ultimi cinquant’anni nelle aree del mondo più afflitte dalla fame, ma l’indice della produzione pro capite, nelle stesse aree, è cambiato ben poco perché la popolazione è cresciuta quasi altrettanto rapidamente. Nel caso dell’Africa, la produzione di cibo pro capite, fra il 1996 e il 2001, è addirittura diminuita del 9%.
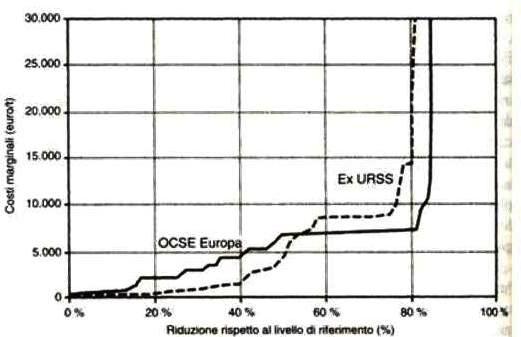
Costi di riduzione inquinamento
È possibile ridurre l’ossido di azoto (NOx) nell’atmosfera in misura significativa e a bassi costi, ma a partire da un certo livello di abbattimento, i costi di ulteriori riduzioni aumentano vertiginosamente.
In estrema sintesi il tema chiave dell’ultimo rapporto in I nuovi limiti dello sviluppo è: il tempo è il vero limite del mondo reale.
«Se ha abbastanza tempo, l’umanità è in grado di risolvere qualunque problema, o quasi. La crescita, e specialmente la crescita esponenziale, è oltremodo insidiosa perché riduce il tempo a disposizione per agire efficacemente. Sollecita un sistema a un ritmo sempre più accelerato, finché le strutture per fronteggiarla, adeguate a tassi di cambiamento più lenti, non cominciano a vacillare.»
Conclusioni
Da quanto qui illustrato, appare evidente come la matematica non solo sia un potente strumento per gli addetti ai lavori, ma funga anche da supporto indispensabile alla trasmissione del sapere. Negli ultimi anni la matematica si è rivelata un potente linguaggio di comunicazione di massa, sempre più spesso usato ed a volte abusato dai media.
Il tema della sostenibilità del pianeta Terra è oggi di grande attualità; ci auguriamo che questa breve nota possa consentire anche ai non esperti di recepire le informazioni con spirito critico ed affrontare la questione con maggiore consapevolezza.
Ci piace concludere con una frase molto significativa di Dennis Meadows: «all any of us can do, day after day, through our work, our science, our teaching, is to try to make things a little better than they would have been otherwise. And I know I can do that».
Bibliografia consultata
Primo Brandi, Anna Salvadori, Matematica&Realtà, Laboratori di innovazione didattica 2006-2007, Università degli Studi di Perugia
Thomas R. Malthus, An Essay on the Principle of the Population as it Affects the Future Improvement of Society, 1798
Donella H. Meadows, Dennis L. Meadows, Jørgen Randers, William W. Behrens III, I limiti dello sviluppo, Mondadori, Milano 1972
Donella H. Meadows, Dennis L. Meadows, Jørgen Randers, Oltre i limiti dello sviluppo, Il Saggiatore, Milano 1993
Donella H. Meadows, Dennis L. Meadows, Jørgen Randers, I nuovi limiti dello sviluppo, Mondadori, Milano 2006
